Practical Significance

Even if an experiment result shows a statistically significant difference in an
evaluation metric between control and experimental groups, that does not
necessarily mean that the experiment was a success. If there are any costs
associated with deploying a change, those costs might outweigh the benefits
expected based on the experiment results. Practical significance refers to
the level of effect that you need to observe in order for the experiment to be
called a true success and implemented in truth. Not all experiments imply a
practical significance boundary, but it's an important factor in the
interpretation of outcomes where it is relevant.

If you consider the confidence interval for an evaluation metric statistic
against the null baseline and practical significance bound, there are a few
cases that can come about.

Confidence interval is fully in practical significance region

(Below, m_0 indicates the null statistic value, d_{min} the practical significance bound, and the blue line the confidence interval for the observed statistic. We assume that we're looking for a positive change, ignoring the negative equivalent for d_{min}.)

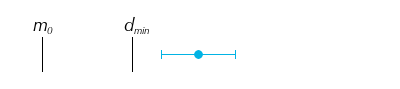
If the confidence interval for the statistic does not include the null or
the practical significance level, then the experimental manipulation can be
concluded to have a statistically and practically significant effect. It is
clearest in this case that the manipulation should be implemented as a success.

Confidence interval completely excludes any part of practical significance region

If the confidence interval does not include any values that would be considered
practically significant, this is a clear case for us to not implement the
experimental change. This includes the case where the metric is statistically
significant, but whose interval does not extend past the practical significance
bounds. With such a low chance of practical significance being achieved on the
metric, we should be wary of implementing the change.

Confidence interval includes points both inside and outside practical significance bounds

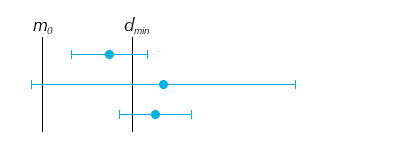
This leaves the trickiest cases to consider, where the confidence interval
straddles the practical significance bound. In each of these cases, there is
an uncertain possibility of practical significance being achieved. In an ideal
world, you would be able to collect more data to reduce our uncertainty,
reducing the scenario to one of the previous cases. Outside of this, you'll
need to consider the risks carefully in order to make a recommendation on
whether or not to follow through with a tested change. Your analysis might also
reveal subsets of the population or aspects of the manipulation that do work,
in order to refine further studies or experiments.

Next Concept